BSP Trees, Part 1: Structure
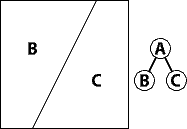
Many games such as Quake use binary space partitioning trees. The purpose of the BSP tree is to partition space into discrete volumes. This is kind of like carving up infinite space into a bunch of smaller chunks. Quake uses a 3D BSP tree, but 2D BSP trees are useful too, and much easier to understand and explain. Doom uses a 2D BSP tree, for example. Here is our starting point, the infinite plane. We will call the infinite plane A.

The infinite plane is very boring, so I have cut it into two pieces. BSP trees are rather strict in that you are only allowed to divide using a straight line that goes as far as possible in each direction. On the left of that line is B, and the right is C. Both B and C are part of A; they are called A’s children.
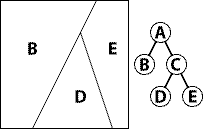
We do the same thing to C to make D and E. Notice how none of it spills over into B — nothing gets bigger, it just gets cut into more and more chunks.
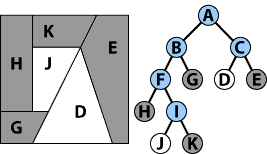
We do it again, this time to B.

Here is a carved up BSP tree. All of the final sections — D, E, G, H, J, and K — are called leaves (although leafs is also seen). All of the sections, carved or no, (A-K) are called nodes. All of the sections that have been carved — A, B, C, F, and I — are called branches.

BSP trees suddenly become more interesting when some of the leaves are labeled solid. Now there is a room with a funny shape that the player can walk around in. Notice that all of the leaves are open or solid, while all of the branches are mixed.